Probability-Impact Chart

The most elementary environmental scanning system can quickly identify more potential events than the largest institution can address. The events must be limited to some manageable number to ensure the organization's effectiveness. This limiting process is achieved by a rigorous, objective evaluation of the events. The goal is to create a process within which the events compete with one another to determine their relative and/or expected importance. The less important events are the focus of continued monitoring and analysis or are used in the forecasting or other stages. The traditional methods of research analysis and forecasting can be used at this stage. Frequently, evaluation of the future impacts of a potential event must rest on opinion, belief, and judgmental forecasts. (Note, the material for this exercise are derived from Morrison, Renfro, and Boucher [1984]).

What is the ability of the institution to effectively anticipate, respond to, and manage the potential event?

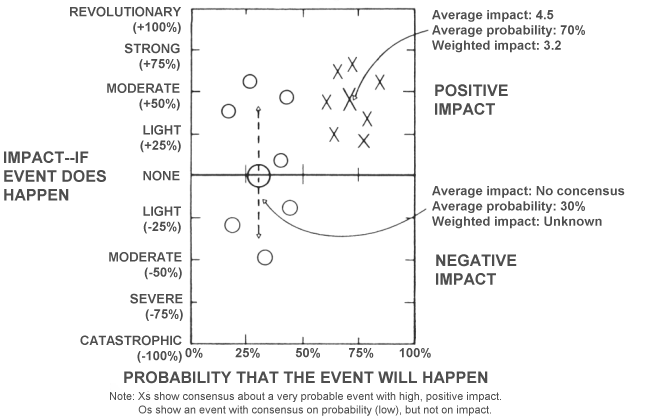
One method of evaluating events identified during scanning involves addressing three separate questions: (1) What is the probability that the event will actually happen during some future period, usually the next decade? (2) Assuming it actually happens, what will its impact be on the future of higher education in the Middle East? (3) What is the ability of an institution to effectively anticipate, respond to, and manage the event? While these questions may appear easy to answer, their use and interpretation in the evaluation process involve care and subtlety. The results for the first two questions are frequently plotted on a simple chart to produce a distribution of probability and impact. Many possible interpretations of the results can easily be displayed on such a chart.

Collecting judgments on an event's probability, impact, and degree of control can be done by using simple questionnaires or interviews and quantifying participants' opinions using various scales (for example, probability can range from 0 to 100, impact from 0 to 10). When all participants have made their forecasts, the next step is to calculate a group average or median score. Quantification is useful because it is fast, and it tends to focus the attention of the group on the subject rather than the source of the estimates.

The next question concerns evaluating the impact of the emerging issue or event, based on the assumption that it actually occurs. Frequently a scale of 0 to 10 is used to provide a range for the answers to this question, where 0 is no impact, 5 is moderate impact, and 10 is catastrophic or severe impact. Usually plus or minus answers can be incorporated. This question and the first question (an event's probability) can be combined in a single chart that displays a probability impact space with positive and negative impacts on the vertical axis and probability from 0 to 100 on the horizontal axis. This chart can be used as a questionnaire in which respondents record their answer to the probability and impact questions by placing a mark on the chart with the coordinates of their opinion about the probability and the impact of the issue. When all of the participants have expressed their opinions, all of the votes can be transferred to a single chart to show the group's opinion. A sample matrix with a group's opinions about an X-event and an O-event is shown in Figure 1. The X-event shows reasonably good consensus that the event will probably happen and that it will have a positive impact; therefore, calculating an average for the group's response is useful and credible. For the O-event, however, the group shows reasonable agreement that the event has low probability of occurring but is split on its probable impact.

FIGURE 1 PROBABILITY-IMPACT CHART SUMMARIZING SEVEN VOTES FOR TWO DIFFERENT EVENTS

Source: Renfro and Morrison 1983a.

The X-event highlights one of the problems of this particular method: Respondents tend to provide answers either from different perspectives or with some inherent net impact where positive impacts cancel or offset negative impacts. In reality, an emerging issue or event often has both positive and negative impacts. Thus, the question should be asked in two parts: What are the positive impacts of this event, and what are its negative impacts? In rank ordering events, two ranks are prepared-one for positive and one for negative events-to permit the development of detailed policies, responses, and strategies based upon a recognition of the dual impacts of most emerging issues. Even with the recognition of an event's dual impact, consensus may be insufficient to identify the average group response. In this case, it may be useful to return the group's opinion to the individual participants for further discussion and reevaluation of the issue. This process of anonymous voting with structured feedback is known as Delphi. Anonymity can be extremely useful. In one private study, for example, all of the participants in the project publicly supported the need to adopt a particular policy for the organization. But when asked to evaluate the policy anonymously on the probability-impact matrix, the respondents indicated that though they believed the policy was likely to be adopted, they did not expect it to have any significant impact. This discovery allowed the decision-makers to avoid the risks and costs of a new policy that was almost certain to fail.

When repeated reevaluations and discussions do not produce sufficient consensus, it may be necessary to redefine the question to evaluate the impact on particular subcategories; subcategories of the institution, for example, would include the impact on personnel, on finances, on curricula, or on faculty. As with all of today's judgmental forecasting techniques, the purpose is to produce useful substantive information about the future and to arrive at a greater understanding of the context, setting, and framework of the evolving future.

The most popular method of interpreting the result of a probability-impact chart is to calculate the weighted positive and negative importance--that is, the product of the average probability and the average (positive and negative) importance--for each event. The events are then ranked according to this weighted importance. Thus, the event ranked as number one is that with the highest combined probability and impact. The other events are listed in descending priority according to their weighted importance.

Ranking the events according to weights calculated in this manner implicitly assumes that the item identified in the scanning is indeed a potential event-that is, one that has an element of surprise. If all of the items identified in scanning are new and emerging and portend this element of surprise (that is, they are unknown to the educational community or at least to the community of the institution now and will remain that way until they emerge with surprise and the potential for upset), then the strategic planning process would do well to focus on those that are most likely to do so and to have the greatest impact. If, however, the issues are not surprises, then another system of evaluating and ranking the events and issues will be necessary. For example, if the entire community knows of a particular event and expects that it will not happen, then this low probability will produce a low priority. Yet, if the event would in fact occur, then it would be of great importance. The surprise then is in the occurrence of the unexpected. The key in this case is the upset expectation. It may be just as much of an upset if an item that everyone expects to occur does not in fact happen. Thus, the evaluation of a probability-impact chart depends on another dimension-that is, one of expectation and awareness. The most important events might be those of high impact and high uncertainty, that is, those centered around the 50 percent probability line. These are the events that are as likely as not to occur and portend an element of surprise for some portion of the community when they happen or do not happen.

Another aspect of events that is often evaluated is their timing, that is, when they are most likely to occur. If an event is evaluated in several rounds, consensus about the probability is often achieved in the early rounds. In the last rounds, timing can be substituted for probability by changing the horizontal axis from 0 to 100 to now to 10 years from now. Then the question becomes, In which of the next 10 years is the event most likely to happen? If necessary, additional questions can explore lead time for an event's occurrence, year of last effective response opportunity, lag time to impact, and so on. All of these factors have been used to evaluate the relative importance of emerging issues and events.

Events that are ranked according to their weighted importance have a built-in assumption that should usually be challenged; that is, the ranking assumes that the administrators and the institution will be equally effective in addressing the implications of all of the events should they occur. This assumption is almost certainly false and seldom of great importance. Suppose that the top priority issue is one on which the institution could have little influence and then only at great cost but that a lower-level item is one on which the institution could have a significant impact with a small investment of resources. It would clearly be foolish to squander great resources for little advantage, when great advantage could be obtained for a much smaller investment. Thus, in addition to the estimation of the weighted importance, the extent to which the event might respond to institutional actions of various costs and difficulty must be evaluated. The cost-effectiveness ratio measures the relative efficiency of alternative institutional actions-actions that are expressions of strategy. This outcome is especially evident when the differences in ratio are small, but if planning for potential events are competing for the same resources, the cost-effectiveness ratios will be essential in guiding the effective use of the institution's limited resources. The top-ranked events may also be important to major administrative functions other than strategic planning.

Probabilty-Impact Chart Exercise

Given that we do not have much time to explore the use of this tool, we will confine our experience to gaining a shared view of the probability and impact of a potential event that could affect the future of colleges and universities in the Middle East. Take one of the top three events identified in the event identification exercise and ask three questions: 

Each person in each group will independently estimate the probability of occurrence and the degree of negative and positive impact on the form provided and then will use the green dots to post his or her votes on the flip chart form. This is a poll. The group facilitator will then lead a discussion of these votes, asking for the rationale underlying the extreme votes. After this discussion, each group member will revote, this time using the red dots. The discussion and revote constitutes a Delphi. The reportback will consist of a discussion/analysis of the Delphi experience regarding the event you used.

Reference

Morrison, J. L., Renfro, W. L., and Boucher, W. I. (1984). Futures Research and the Strategic Planning Process. ASHE/ERIC Clearinghouse on Higher Education Research Report Series Number 9.